Lots of the slot games you can play online today are out of this world. We don’t just mean they showcase phenomenal graphics, brilliant bonus features, and big winning potential. We mean they’re literally set out of this world – in galaxies far, far away – with more aliens and rocket ships than you can blast a laser beam at!
Here are 5 of the best space-themed slots you can play at bgo.com, the online casino boasting over 600 slot, jackpot and live casino games. Try them out today and discover which is your favorite.
Money Mad Martians: Cosmic Cash

Before it landed on the online gaming scene, Money Mad Martians: Cosmic Cash used to be a popular slot machine in real pubs and casinos. It’s themed around aliens from the planet Mars and comes with 3 main bonus features. The first is the Shuffling Reels Feature, which can see mad Martians fly in after any losing spin to move symbols around on the reels and create winning combinations. The second is the Asteroid Bonus, where you get to blast matter floating about in space for prizes. And finally, you have what would think is the game’s best bonus feature of all: the Planet Bonus. Here you get to try and blow up entire planets to win some seriously big cash payouts!
Alien Robots

Think you’ve got what it takes to brave intergalactic cyborgs? Then you need to play Alien Robots. It’s a futuristic slot boasting 243 ways to win on every spin and lots of funky cartoon androids from foreign planets. What we think what makes this slot so great is its Free Spins Bonus. Spot 3, 4 or 5 UFOs on the reels at once and you’ll be awarded up to 50 Free Spins! There’s also a Sticky Wilds Feature that kicks in throughout all Free Spins. Whenever a substituting Wild symbol is landed, it expands to cover the entire reel and becomes ‘sticky’ – by which we mean it’s held in place as the reels are re-spun for an even better chance to win!
Cowboys & Aliens

There’s nothing we love more than teaming up with lasso-wielding cowboys to defend the Wild West from alien life. If you feel the same, you’ll not want to miss playing Cowboys & Aliens. It’s a 9-payline slot designed with comic-book-style graphics and some seriously-cool bonus features. The Alien Weapon Feature is triggered whenever a space gun is landed on the first reel. Watch as shots are fired at random symbols on the reels, turning them into Wilds with the power to complete more winning combinations! There’s also a Free Games Bonus and an Alien Attack Bonus, where you’ll get to kill aliens for cash.
Space Wars

Though you may not be aware of it, there’s been a war raging between the inhabitants of different planets for centuries. Space Wars is a slot that gives you a chance to join in the intergalactic battle. If we had to pick what we love most about this slot, it would have to be the Cloning Pod you can see beside the reels as you play. Winning symbols get blasted into the Cloning Pod after every successful spin, only to be duplicated and shot back out as the reels are re-spun to boost your chances of landing another win!
Astro Babes
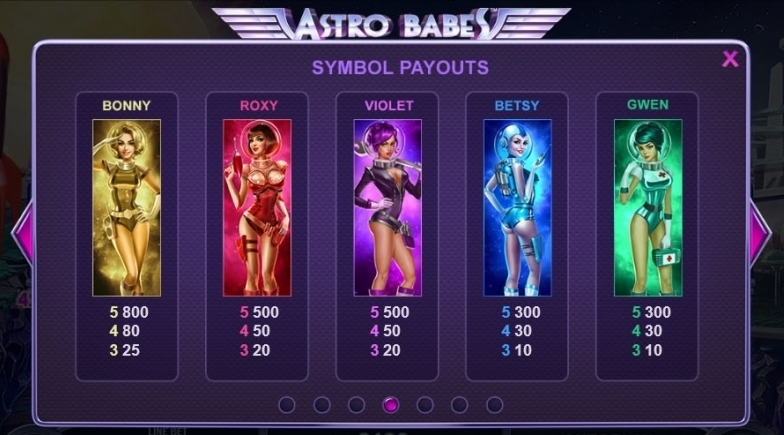
If you haven’t met them already, let us introduce you to the Astro Babes. Bonny, Roxy, Violet, Betsy, and Gwen are the 5 girls that form a group of smoking-hot astronauts with their own 100-payline slot. The ladies are more than just eye candy for players. As you spin, you’ll notice that each babe can fill an entire reel to turn it into a special Wild Reel, helping you to land more winning combinations! So even though there’s not an alien in sight, we think it one of the best space-themed slots around.
